RESUMEN. Efectuamos la representación gráfica de la campana de Gauss.
Enunciado.
Representar gráficamente la campana de Gauss, es decir la gráfica de la función $$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\dfrac{-\frac{1}{2}(x-\mu)^2}{\sigma^2}}.$$
Solución. Representaremos la gráfica de la función $$g(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\dfrac{-\frac{1}{2}x^2}{\sigma^2}},$$ con lo cual la gráfica de $f(x)$ se obtendrá trasladando a la derecha la de $g(x)$ en una cantidad $\mu.$ Claramente el dominio de $g(x)$ es $\mathbb{R}$ y $g(x)$ es par (simétrica respecto del eje de ordenadas). Se verifica de manera inmediata que $\lim_{x\to -\infty}g(x)=\lim_{x\to +\infty}g(x)=0,$ es decir $y=0$ es asíntota horizontal. La derivada de $g(x)$ es $$g^\prime (x)=\frac{1}{\sqrt{2\pi}\sigma}e^{\dfrac{-\frac{1}{2}x^2}{\sigma^2}}\left(-\frac{x}{\sigma^2}\right)=-\frac{1}{\sqrt{2\pi}\sigma^3}e^{\dfrac{-\frac{1}{2}x^2}{\sigma^2}}\cdot x$$ que se anula exáctamente en $x=0.$ Si $x < 0$ se verifica $f^\prime (x) > 0 $ (estríctamente creciente) y si $x > 0$ se verifica $f^\prime (x) < 0 $ (estríctamente decreciente), por tanto en $x=0$ tenemos un máximo absoluto. La segunda derivada de $g(x)$ es $$g^{\prime\prime}(x)=-\frac{1}{\sqrt{2\pi}\sigma^3}\left[e^{\dfrac{-\frac{1}{2}x^2}{\sigma^2}}\cdot \frac{-x}{\sigma^2}\cdot x+e^{\dfrac{-\frac{1}{2}x^2}{\sigma^2}}\cdot 1\right]$$ $$=\frac{1}{\sqrt{2\pi}\sigma^3}e^{\dfrac{-\frac{1}{2}x^2}{\sigma^2}}\left(\frac{x^2}{\sigma^2}-1\right)=\frac{1}{\sqrt{2\pi}\sigma^5}e^{\dfrac{-\frac{1}{2}x^2}{\sigma^2}}\left(x^2-\sigma^2\right).$$ La segunda derivada de $g(x)$ se anula exáctamente en $x=\pm \sigma$ y debido a la paridad de $g$ sólo estudiamos el comportamiento para $x>0.$ Si $0 < x < \sigma$ se verifica $ g^{\prime\prime} (x) < 0$ (cóncava hacia abajo) y si $x > \sigma$, $ g^{\prime\prime} (x) > 0$ (cóncava hacia arriba) por tanto hay dos puntos de inflexión en $x\pm \sigma$.
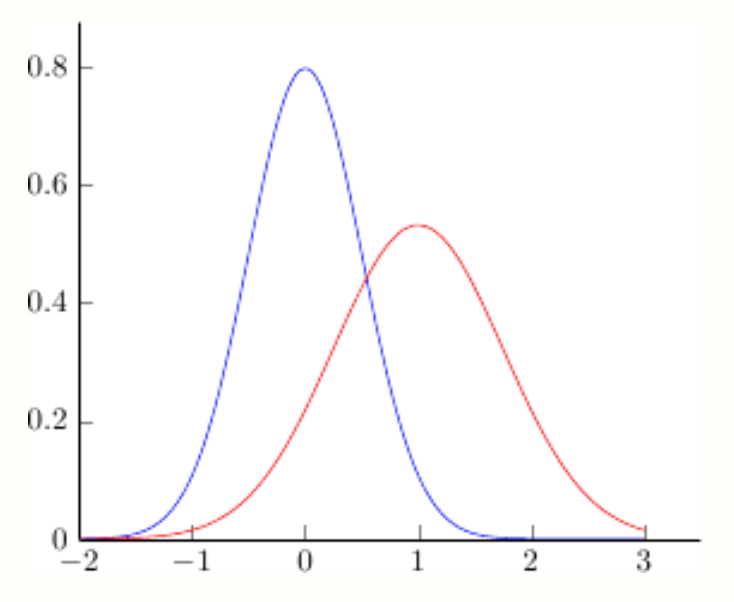
En la siguiente figura aparece en azul la gráfica de $g(x)$ para un determinado $\sigma$ y en rojo la de $f(x)$ para un $\mu > 0$ y un determinado $\sigma.$